0.1+0.2=0.30000000000000004❓

发表于   |   分类于   |     |   阅读次数


JavaScript中所有的数字，无论是整数还是小数，其类型都是 Number，遵循 IEEE 754 程序内部用一个 64 位固定长度的二进制进行存储表示。JavaScript 中的浮点数进行运算时，经常会遇到计算精度问题，例如经典的 0.1+0.2=0.30000000000000004，本文将探究 JavaScript 的浮点数，并解释为何 0.1+0.2=0.30000000000000004

浮点数的二进制表示

JavaScript 里的数字是采用 IEEE 754 标准的 64 位 double 双精度浮点数（与之相关的还有 32 位 float 单精度浮点数）。该规范定义了浮点数的格式。

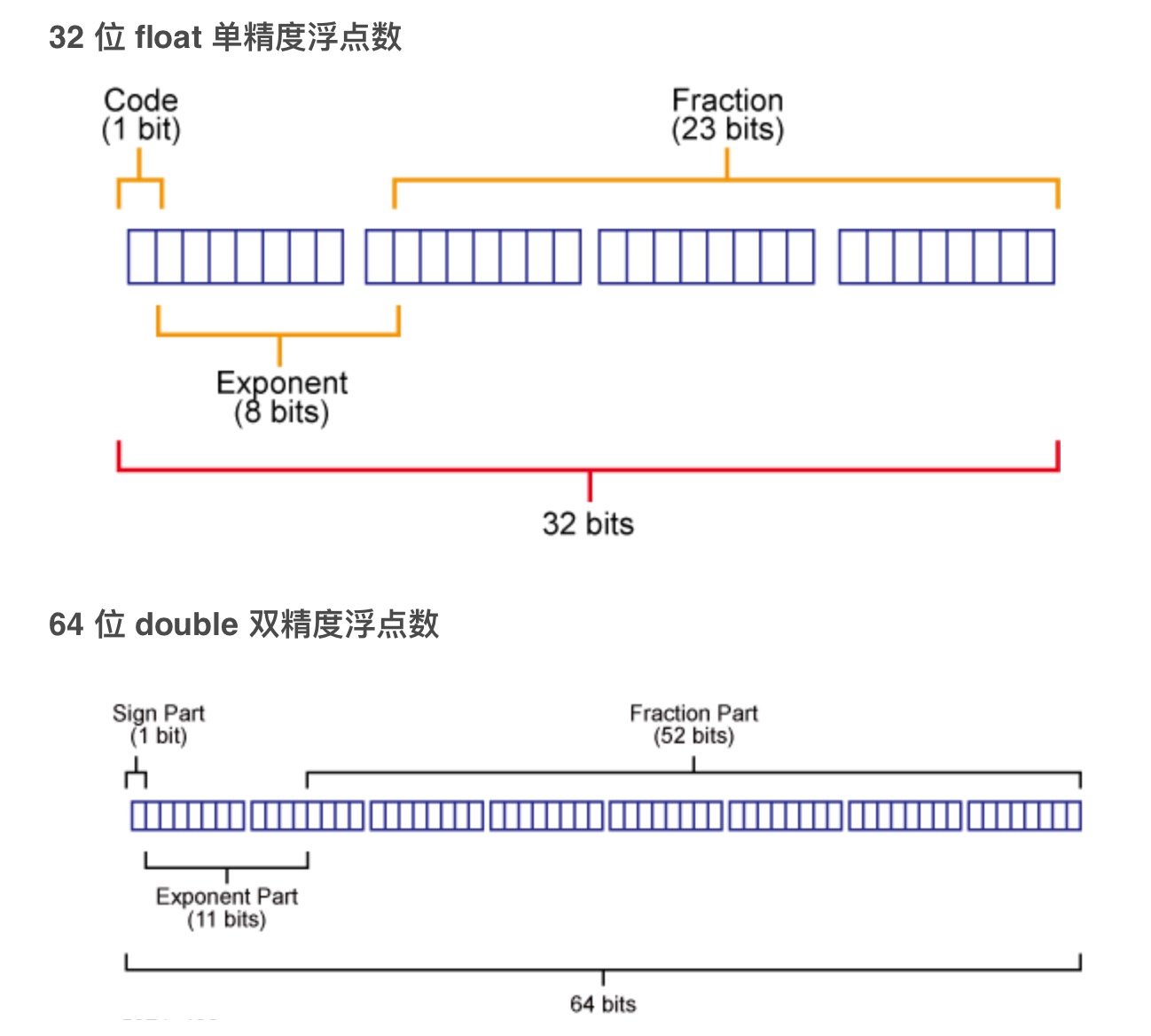
对于 32 位的浮点数，最高的 1 位是符号位 S，接着的 8 位是指数 E，剩下的 23 位为尾数位 M
对于 64 位的浮点数，最高的 1 位是符号位 S，接着的 11 位是指数 E，剩下的 52 位为尾数位 M

  • 符号位 S：0 表示正数，1 表示负数
  • 指数 E：表示次方
  • 尾数位 M：表示有效数字（小数部分）

实际数字的计算公式为：

1
V = (-1)^S * M * 2^E

接下来只对 64 位浮点数的二进制表示进行分析：

该计算公式遵循科学计数法的规范，对于十进制表示而言，尾数的范围是 0<M<10；对于二进制表示而言，尾数的范围是 0<M<2。浮点数二进制表示，所以此处尾数的范围是：0<M<2，也就是说 M 的整数位始终是 1，所以可以舍去，只保留后面的小数部分，这样就能表示 53 位了。

指数位 E 是一个无符号整数，64 位浮点数中，指数位长度是 11 位，取值范围是 [0~2047]，由于科学计数法中指数可正可负，所以，中间数 1023，[0,1022] 表示为负，[1024,2047] 表示为正

最终的公式变成：

1
V = (-1)^S * (M + 1) * 2^(E - 1023)

十进制转换为二进制

十进制整数转换为二进制整数：采用”除2取余，逆序排列”法。具体做法是：用 2 去除十进制整数，可以得到一个商和余数；再用 2 去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

十进制小数转换成二进制小数：采用”乘2取整，顺序排列”法。具体做法是：用 2 乘十进制小数，可以得到积，将积的整数部分取出，再用 2 乘余下的小数 部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

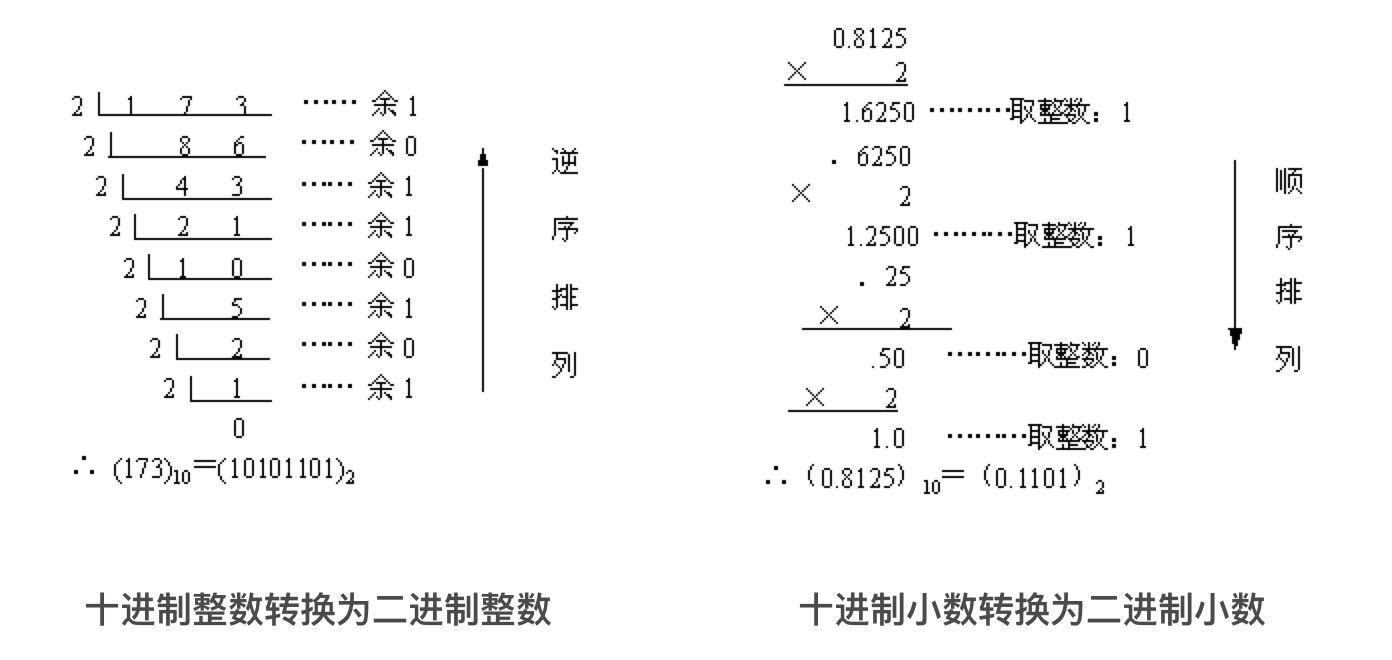
（173.8125）10＝（❓）2

  • （173）10＝（10101101）2
  • （0.8125）10＝（0.1101）2

把整数部分和小数部分合并得：（173.8125）10＝（10101101.1101）2

64 位浮点数的二进制表示

十进制数和 64 位浮点数二进制相互转换可以访问该网站进行：
http://www.binaryconvert.com/convert_double.html

下面以 0.1 为例，对其进行 64 位二进制表示

0.1 转换成二进制：0.0001100110011001100(1100循环)，即 1.100110011001100x2^-4，得到:

  • 指数位 E = -4 + 1023 = 1019 (1019 11 位二进制表示为：01111111011)
  • 尾数位 M = 100110011001100… (舍去首位 1)

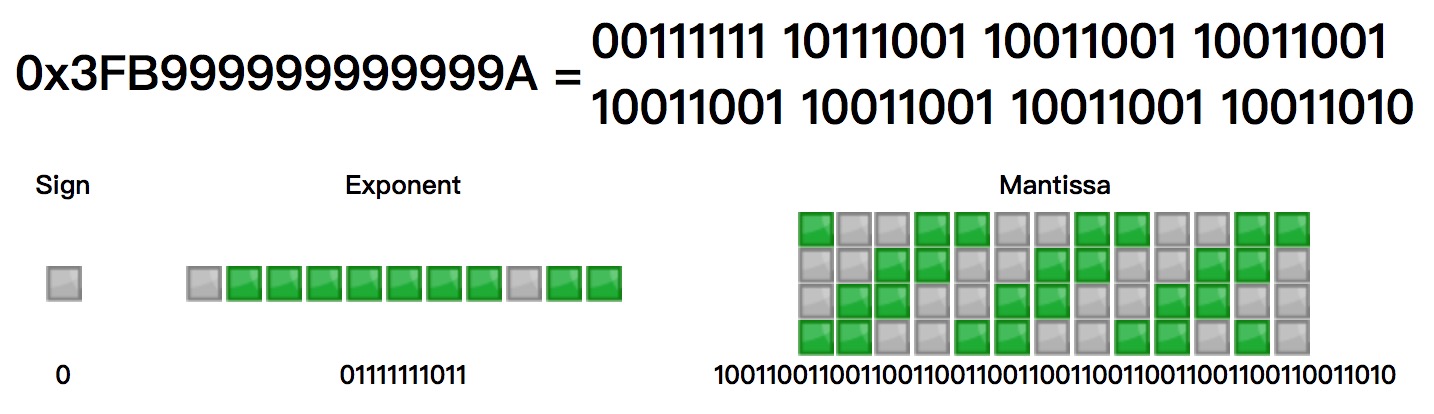
所以十进制 0.1 转换成 64 位浮点数二进制表示为：

1
0011111110111001100110011001100110011001100110011001100110011010

而将 64 位浮点数二进制的 0.1 转换回十进制时，得到：1.00000000000000005551115123126E-1。

但是：此时输出 x 为啥能得到 0.1 呢？

1
2
var x = 0.1
console.log(x) // -> 0.1

分析：尾数位固定长度 52 位，加上省略的整数位 1，就再加上一位，那么尾数最多能表示的数为：2^53=9007199254740992，对应的十进制科学计数尾数是 9.007199254740992，这也是 JavaScript 最多能表示的精度，长度是 16，所以用 toPrecision(16) 来做精度运算，于是：

1
0.10000000000000000555.toPrecision(16) // -> 0.1

如果使用更高精度，那么可能得到的就不是 0.1

1
2
var x = 0.1
console.log(x.toPrecision(21)) // -> 0.100000000000000005551

注意：toPrecision 方法最大指定精度为 21。对于 0.1 而言，64 位二进制表示，最多能表示的精度为 16 位；转换成十进制后 0.100000000000000005551，默认的 JavaScript 使用 16 位进行截取，我们最多能使用 21 位进行截取，注意二者的区别。

toPrecision 和 toFixed

  • toPrecision 方法以指定的精度返回该数值对象的字符串表示，精度是从左至右第一个不为0的数开始数起
  • toFixed 方法使用定点表示法来格式化一个数，是小数点后指定位数取整，从小数点开始数起
1
2
3
4
5
var x = 0.12345
x.toPrecision(3) // -> "0.123"
var y = 1.234
y.toFixed(3) // -> "1.234"

这两个方法在截取数字时，都有进行四舍五入处理，但是都存在 BUG，使用要谨慎❗️

1
2
3
4
5
6
7
8
var x = 0.3456
x.toPrecision(3) // -> "0.346"
x.toFixed(3) // -> "0.346"
// BUG
var y = 1.005
y.toPrecision(3) // -> "1.00"
y.toFixed(2) // -> "1.00"

原因是：1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去了

0.1+0.2=0.30000000000000004

在计算 0.1+0.2 的时候，现将其转换为二进制，得到的结果也是二进制，然后再将其转换为十进制

1
2
3
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

计算结果 0.0100110011001100110011001100110011001100110011001100111 转换成十进制，就是 0.30000000000000004，这就导致出现了误差。

遇到浮点数误差问题时可以直接使用 dt-fe/number-precision 完美支持浮点数的加减乘除、四舍五入等运算。

数值范围

根据浮点数算术标准，指数位最大值为 2047，E = 2047 -1023 = 1024，所以 JavaScript 能表示的数值范围是：[-(2^1024-1), +(2^1024-1)]，即：正负1.7976931348623157乘以10的308次方，注意：

1
2
3
4
5
Math.pow(2, 1023)
-> 8.98846567431158e+307
Math.pow(2, 1024)
-> Infinity

注意：

  • Number.MIN_VALUE 属性表示在 JavaScript 中所能表示的最小的正值
    • 值为 5e-324
    • MIN_VALUE 属性是 JavaScript 里最接近 0 的正值，而不是最小的负值
    • 小于 MIN_VALUE 的值将会转换为 0
  • Number.MAX_VALUE 属性表示在 JavaScript 里所能表示的最大数值
    • 值为 1.7976931348623157e+308
    • 大于 MAX_VALUE 的值代表 “Infinity”

JavaScript 规定能安全的表示数字(进行精确算术运算)的范围在 ：[-2^53, +2^53]，即正负2的53次方；对于超过这个范围的整数，JavaScript 依旧可以进行运算，但却不保证运算结果的准确性，这也是 JavaScript 中安全整数的两个边界：Number.MIN_SAFE_INTEGER 和 Number.MAX_SAFE_INTEGER。

1
2
3
4
5
Number.MIN_SAFE_INTEGER
-> -9007199254740991
Number.MAX_SAFE_INTEGER
-> 9007199254740991

超过安全整数范围的，计算不保证正确，例如：

1
2
3
4
5
6
Math.pow(2, 53)
-> 9007199254740992
Math.pow(2, 53) + 1
-> 9007199254740992
Math.pow(2, 53) + 2
-> 9007199254740994

对于不在 [-2^53, +2^53] 范围中的数字，例如 (2^53, 2^63) 之间的数会出现什么情况呢？

  • (2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
  • (2^54, 2^55) 之间的数会四个选一个，只能精确表示4的倍数
  • … 依次跳过更多2的倍数

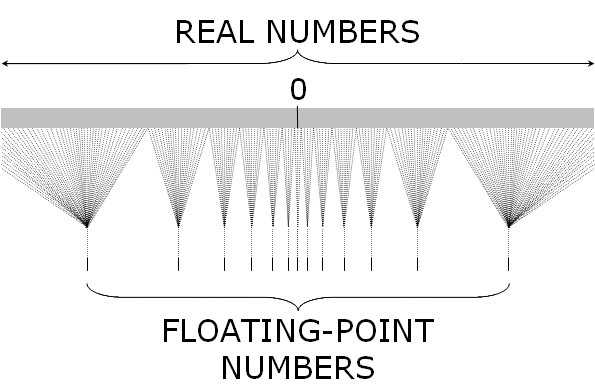
下面这张图能很好的表示 JavaScript 中浮点数和实数（Real Number）之间的对应关系，我们常用的 [-2^53, 2^53] 只是最中间非常小的一部分，越往两边越稀疏越不精确。

参考链接

JavaScript 浮点数陷阱及解法