SharedPen 之区间树优化

发表于   |   分类于   |     |   阅读次数

前文 SharedPen 之 AnnotationList 讲到：

为了管理，操作整个富文本文档流，我们引入 AnnotationList 单链表结构，把每一段富文本当成 Node 节点，由此形成链表结构。

单链表数据结构形象容易理解，但是执行操作（增删改查）的效率比较低，所有操作的算法复杂度都是 O(N)（其中N为节点数）；优化的方向是将链表数据结构改造成树形结构。本文将对优化思路进行分析。

红黑树

二叉查找树（Binary Search Tree，简称BST）是一棵二叉树，特点是：它的左子节点的值比父节点的值要小，右节点的值要比父节点的值大。它的高度决定了它的查找效率。在理想的情况下，二叉查找树增删查改的时间复杂度为 O(logN)，最坏的情况下为 O(N)。当它的高度为 logN+1 时，我们就说二叉查找树是平衡的。

由于 BST 存在的问题，产生了一种新的树 – 自平衡二叉查找树，自平衡树在插入和删除节点的时候，会通过旋转操作将高度保持在 logN，所以它可以在 O(log N) 时间内做查找，插入和删除。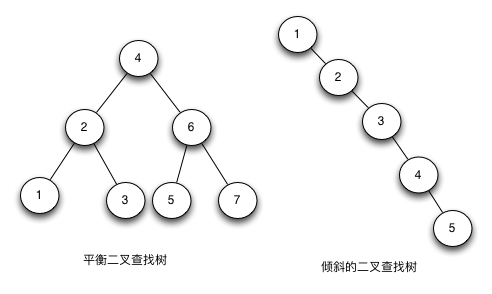

红黑树（Red–black tree）就是一种自平衡二叉查找树，它是复杂的，
但它的操作有着良好的最坏情况运行时间，并且在实践中是高效的，其实际应用也非常广泛。

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。除二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

  • 节点是红色或黑色。
  • 根是黑色。
  • 所有叶子都是黑色（叶子是NIL节点）。
  • 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
  • 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

下面是一个具体的红黑树的图例：

推荐一个数据结构可视化在线工具，可以辅助理解：Data Structure Visualizations
其中红黑树增删节点可视化：Red/Black Tree

区间树

区间树（interval tree）是一种扩展的红黑树，区间树中的节点都代表一个区间。例如区间：(2, 8) (6, 15) (30, 36) (20, 25) (33, 40) 构成如下区间树：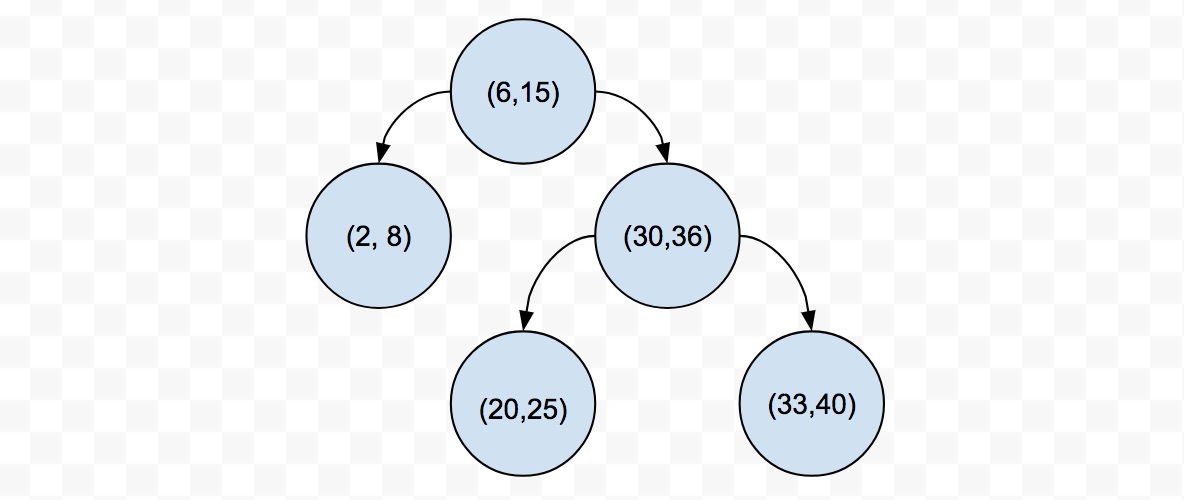

对于一个区间：

  • 区间用 Range(lowerPosition, upperPosition) 来表示，其中：lowerPosition 和 upperPosition 分别表示起始位置和结束位置
  • 在起始和结束位置上，都有两种情况：包含或者不包含，也就是区间的开闭，一共有四种情况：[a, b)，[a, b]，(a, b)，(a, b]

在处理 SharedPen 文本区间时：

  • 注意到我们的区间是连续的（这是区间树的一种特殊情况），所以可以定义我们的区间为：左闭右开，即 [a, b)
  • 区间树也符合二叉查找树的特点，区间进行大小比较时，定义如下：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    class RangeKeyword {
      constructor(lowerPosition, upperPosition) {
        this._lowerPosition = lowerPosition;
        this._upperPosition = upperPosition;
      }
      gt(hint) {
        if (this._lowerPosition == hint._lowerPosition) {
          return this._upperPosition > hint._upperPosition
        }
        return this._lowerPosition > hint._lowerPosition
      }
      lt(hint) {
        if (this._lowerPosition == hint._lowerPosition) {
          return this._upperPosition < hint._upperPosition
        }
        return this._lowerPosition < hint._lowerPosition
      }
      eq(hint) {
        return this._lowerPosition == hint._lowerPosition
          && this._upperPosition == hint._upperPosition
      }
    }

接下来将以这种连续（左闭右开）区间进行分析

区间树有两个重要操作：expand 和 remove

  • 扩张：expand(pos, length)
    在 pos 位置，插入 length 长度的字符，插入文本后，后续的区间位置需要自动更新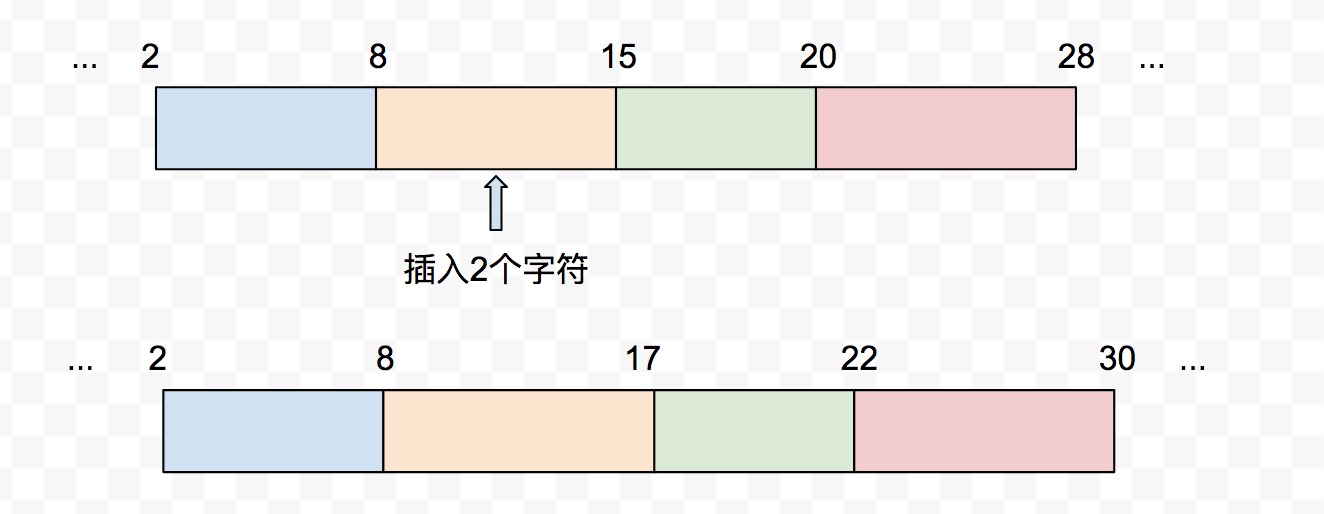

    例子中区间：[2, 8),[8, 15),[15, 20),[20, 28) 变成 [2, 8),[8, 17),[17, 22),[22, 30)
  • 收缩：remove(pos, length)：
    在 pos 位置，删除 length 长度的字符，删除文本后，后续的区间位置需要自动更新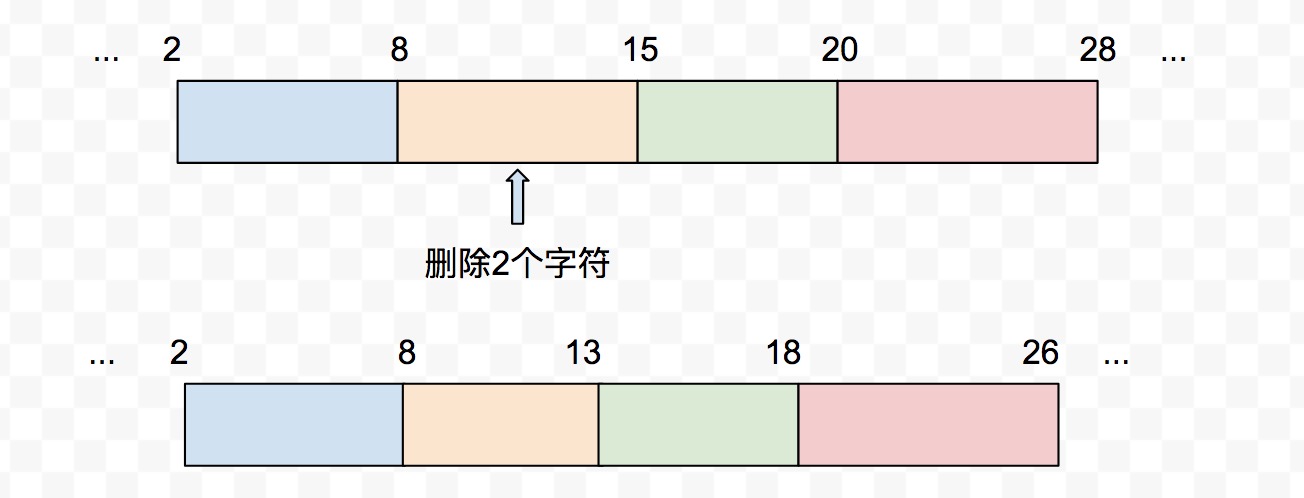

    例子中区间：[2, 8),[8, 15),[15, 20),[20, 28) 变成 [2, 8),[8, 13),[13, 18),[18, 26)

注意到插入和删除文本后，其后续区间的位置都能自动更新，为了实现这个功能，我们需要对区间进行一些处理。区间Range(lowerPosition, upperPosition) 的 lowerPosition 和 upperPosition 都表示绝对位置，下面给区间引入相对位置的概念。

  • 每一个区间都是相对于某一个区间而言的，这个相对的区间称之为 originNode，注意：
    • 左节点的 originNode = 其父节点的 originNode
    • 右节点的 originNode = 其父节点
  • 区间新增的几个属性：
    • origin: 表示区间相对位置的相对起点
    • relativeLower: 表示区间相对位置的起始位置
    • upperDistance: 表示区间的长度

下面通过：[2, 8),[8, 15),[15, 20),[20, 28),[28, 40) 这个区间树来解释一下相对位置的概念

下图中的红色箭头指向为 originNode，注意到其中的 [2, 8) 和 [8, 15) 区间其实是指向这个区间树，表示其相对区间为区间树的起点。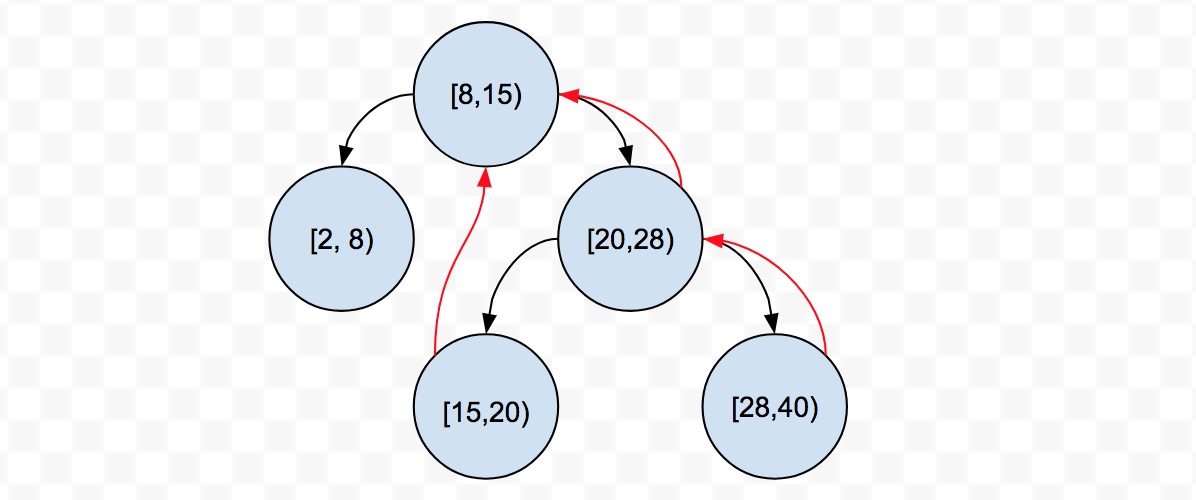

下图中分别列出了每个区间的 origin，relativeLower，upperDistance 的属性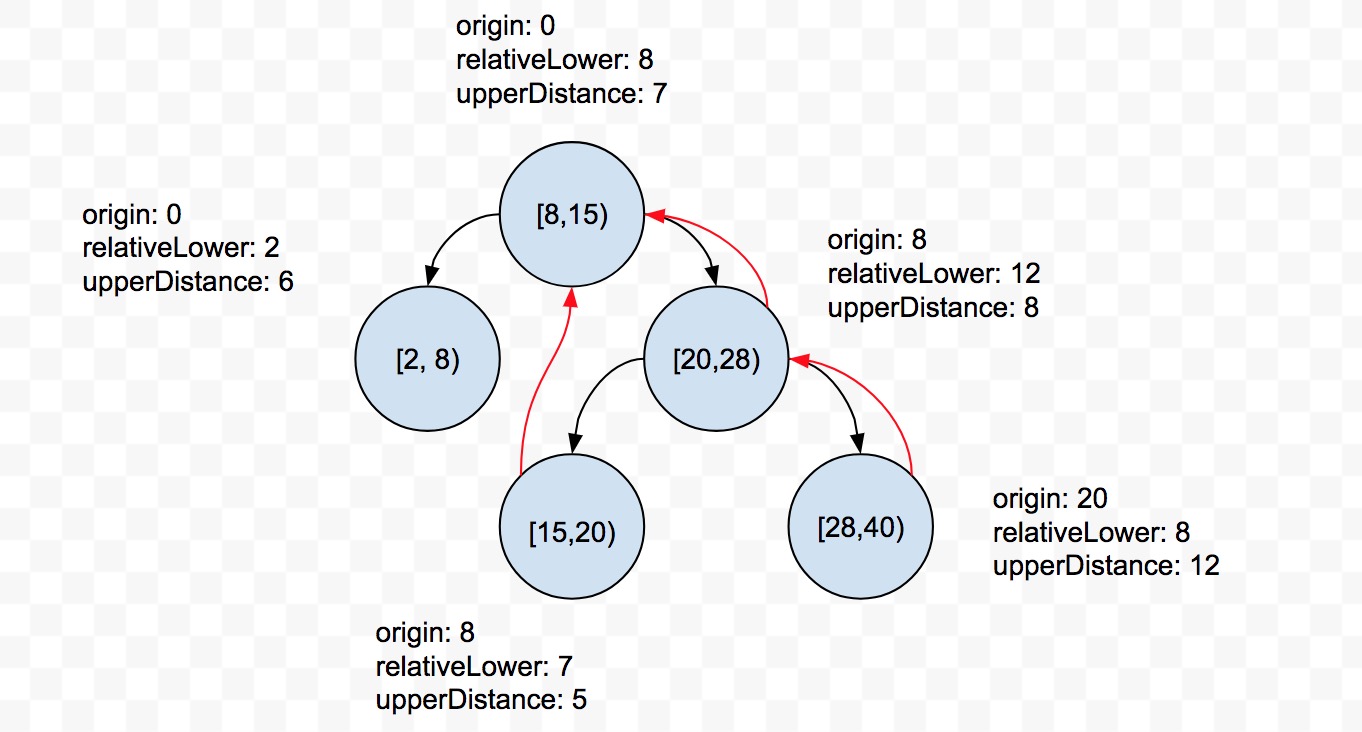

其中区间 origin 属性通过如下计算得到：

1
2
3
4
5
6
7
8
get origin() {
  let n = null,
      o = 0;
  for (n = this.originNode; null != n; n = n.originNode) {
    o += n.relativeLower;
  }
  return o;
}

区间的绝对位置可以通过如下计算得到：

1
2
3
4
5
6
get lowerPosition() {
  return this.origin + this.relativeLower;
}
get upperPosition() {
  return this.lowerPosition + this.upperDistance;
}

有了相对位置概念之后，处理扩张/收缩，只需遍历区间树中的部分节点，更新其中相关的属性即可。如下区间树，expand(10, 2)，在 10 的位置扩展 2 个长度，即区间 [8, 15) 变成 [8, 17)，除了更新当前区间 [8, 15) 外，只需要更新那些以该区间节点为 originNode 的区间，我们可以知道区间 [15, 20) 和 [20, 28) 的 originNode 就是 [8, 15)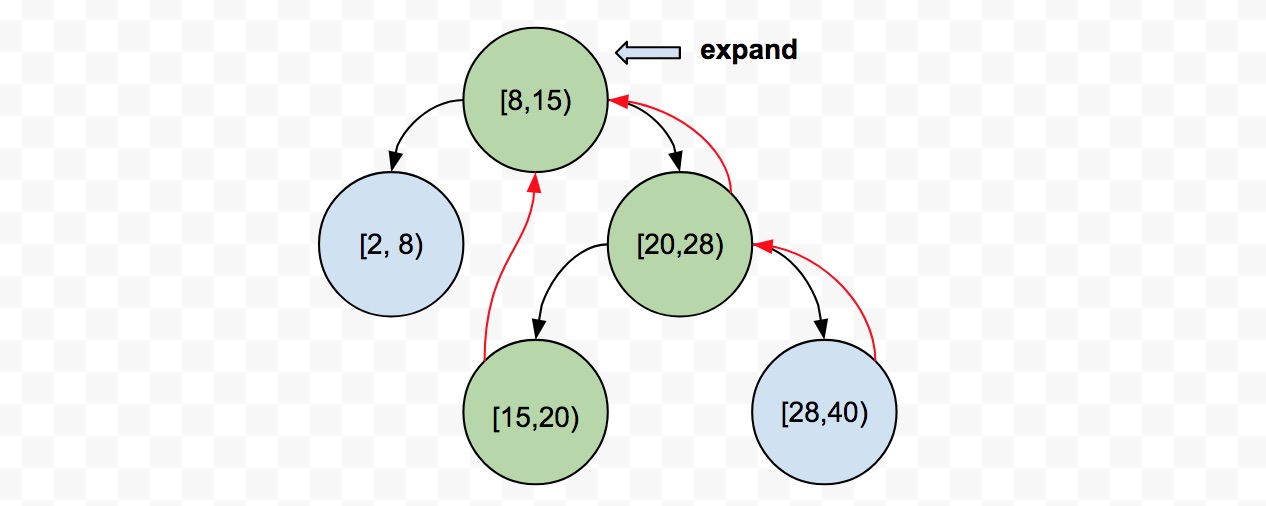

下面简单的介绍一下实现原理：
① passWhole 和 passRight
执行遍历过程中，需要对比执行操作点（插入点/删除点）和区间节点的关系，其中包含两个重要的比较过程：passWhole 和 passRight

  • passWhole
    区间节点有一个 limitPosition 属性，表示当前区间节点所在子树的右边界位置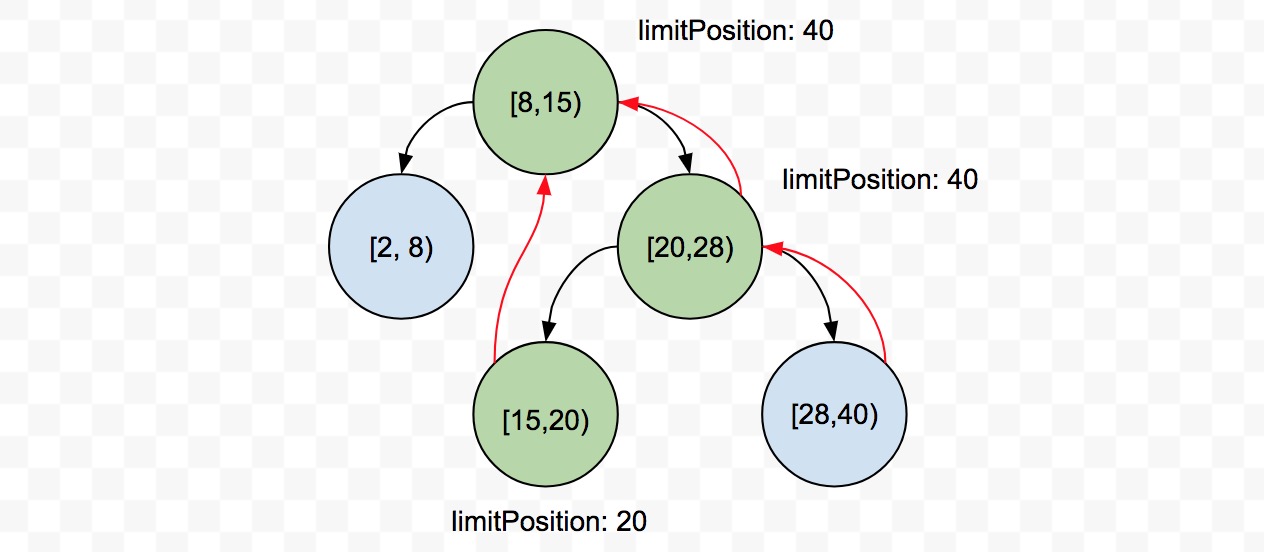

    passWhole 判断执行操作点的位置如果比当前区间节点所在子树的右边界大，那么可以跳过这个子树

    1
    2
    3
    passWhole(hint) {
      return this._position > hint.limitPosition;
    }

  • passRight
    passRight 判断执行操作点的位置如果比当前区间的（绝对位置的）起始位置小，那么可以跳过这个区间节点对应的右子树（即只需考虑当前区间的左子树）

    1
    2
    3
    passRight(hint) {
      return this._position < hint._lowerPosition
    }

② 伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
function travel() {
  var deep = []
  var hint = makeHintAtTree() // 生成区间树迭代器
  var isHintStop = false
  while (true) {
    if (isHintStop) { //
      isHintStop = false
      if (0 == deep.length) {
        break
      }
      // 出栈
      hint = deep.pop()
      // 修改迭代器对应的区间节点数据
      hint._node.visit()
      // 迭代器向左移动
      hint.moveLeft();
    }
    else {
      // 跳过当前区间所在的整颗子树
      if (visitor.passWhole(hint)) {
        isHintStop = true
        continue;
      }
      // 入栈
      deep.push(hint.clone());
      // 跳过当前区间所在的右子树
      if (visitor.passRight(hint)) {
        isHintStop = true
        continue;
      }
      // 迭代器向右移动
      hint.moveRight();
    }
  }
}

AnnotationTree

区间树主要提供四个接口：插入/删除区间；扩张/收缩区间；下面我们通过这四个接口来构建 AnnotationTree，也即是将单链表数据结构的 AnnotationList 改造成区间树数据结构的 AnnotationTree，同样 AnnotationTree 需要提供增删改查的四个功能。

给区间树引入迭代器 Hint(tree, node, origin)，这个迭代器指向区间树的某个节点，迭代器通过 moveLeft，moveRight，movePrev，moveNext，moveUp 方法在区间树中移动游走，迭代器移动过程中会更新保存 origin 信息，方便使用

基础方法

查找 find(tree, pos)

find(tree, pos)：根据位置在区间树中查找区间，返回对应迭代器
区间和位置点的大小比较，定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class PositionKeyword {
  constructor(position) {
    this._position = position
  }
  gt(hint) {
    return this._position >= hint._upperPosition
  }
  lt(hint) {
    return this._position < hint._lowerPosition
  }
  eq(hint) {
    return (hint._lowerPosition <= this._position &&
      this._position < hint._upperPosition)
  }
}

注意：区间是左闭右开，所以当 lowerPosition <= position < upperPosition 时，判断为相等

区间收缩 remove(tree, hint, pos, length)

扩张直接调用区间树的 expand 方法即可；但是对于收缩，调用区间树 remove 方法后，有可能出现长度为 0 的区间，这个时候，我们还需要将长度为 0 的区间进行移除。例如：
区间树：[2, 8),[8, 15),[15, 20),[20, 28),[28, 40)
➡️ 调用区间树方法 remove(10, 13)
区间树变成：[2, 8),[8, 10),[10, 10),[10, 15),[15, 27)
➡️ 移除长度为 0 的区间
区间树变成：[2, 8),[8, 10),[10, 15),[15, 27)

分裂 split(tree, hint, distance, prop)

将 hint 指向的区间节点，在 distance 位置进行分裂，并将 prop 数据附加到左侧节点，返回左侧区间节点迭代器；例如将区间 [15, 20) 分裂成 [15, 17) 和 [17, 20)

❗️注意此时不能将 [15, 20) 收缩变成 [15, 17)，然后再插入新的区间节点 [17, 20)；
因为 [15, 20) 收缩变成 [15, 17)
过程中会调整区间节点的相对位置；而插入新的区间节点并不会调整区间节点的位置关系。例如：
区间树：[2, 8),[8, 15),[15, 20),[20, 28),[28, 40)
➡️ 调用区间树方法 remove(15, 3)
区间树变成：[2, 8),[8, 15),[15, 17),[17, 25),[25, 37)
➡️ 插入新的区间节点 [17, 20)
区间树变成：[2, 8),[8, 15),[15, 17),[17, 20),[17, 25),[25, 37)

正确的做法是：删除当前节点，插入两个新的节点

合并 merge(tree, hint)

将迭代器指向的区间合入下一个区间
做法是：移除当前区间节点和下一区间节点，插入一个新的区间节点

增删改查方法

增删改方法逻辑参考如下代码即可理解；查询方法比较简单，此处略。

插入 insert(pos, length, prop)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
insert(pos, length, prop) {
  // 查找位置对应的迭代器
  var found = this.find(this.tree, pos)
  if (!found) { throw new Error('Not found') }
  if (found._lowerPosition === pos) { // 情况1: 在两句之间插入（注意区间左闭右开）
    if (this.equaler(found, prop)) { // 情况1.1: 和后一句属性相同
      this.expand(this.tree, pos, length)
      return found
    } else {
      // found 移动到前一句
      found.movePrev()
      if (!found.atTree() && this.equaler(found, prop)) { // 情况1.2: 和前一句属性相同
        this.expand(pos-1, length)
        return found
      } else { // 情况1.3: 和前后句都不相同，那么创建新的句
        found.moveNext()
        this.expand(this.tree, pos, length)
        found = this.split(this.tree, found, length, prop)
        return found
      }
    }
  } else { // 情况2: 在一句的中间插入
    if (this.equaler(found, prop)) { // 情况2.2: 句属性相同
      this.expand(this.tree, pos, length)
      return found
    } else { // 情况2.3: 句属性不同 -> 断句，插入新节点
      let _splitDistance = pos - found._lowerPosition
      found = this.split(this.tree, found, _splitDistance, found._node.prop)
      this.expand(this.tree, pos, length)
      found.moveNext()
      found = this.split(this.tree, found, length, prop)
      return found
    }
  }
}

删除 shrink(pos, length)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
shrink(pos, length) {
  // 查找位置对应的迭代器
  var found = this.find(this.tree, pos)
  if (!found) { throw new Error('Not found') }
  if (found._lowerPosition !== pos) { // 删除位置不在句头，先断句
    let _splitDistance = pos - found._lowerPosition
    found = this.split(this.tree, found, _splitDistance, found._node.prop)
  } else { // 删除位置恰好在句头
    found.movePrev()
  }
  // 删除
  this.remove(this.tree, found.clone(), pos, length)
  if (!found.atTree()) {
    var found2 = found.clone()
    found2.moveNext()
    // 判断是否需要和后一句合并
    if (!found2.atTree() && this.equaler(found, found2._node.prop)) {
      this.merge(this.tree, found)
    }
  }

修改 modifyProp(pos, length, propFn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
modifyProp(pos, length, propFn) { // propFn：区间属性修改回调方法
  // 查找位置对应的迭代器
  var found = this.find(this.tree, pos)
  if (!found) { throw new Error('Not found') }
  while(!found.atTree()) {
    let _lower = found._lowerPosition
    let _upper = found._upperPosition
    let _newProp = propFn(found._node.prop) // 返回新的区间属性
    if (!this.equaler(found, _newProp)) {
      if (_lower < pos) {
        found = this.split(tree, found, pos-_lower, found._node.prop)
        found.moveNext()
      }
      if (pos+length < _upper) {
        found = this.split(tree, found, pos+length-found._lowerPosition, found._node.prop)
      }
      // 修改句属性
      found._node.modifyProp(_newProp)
      // 当改变区域和上一个区域交接时，尝试向前合并
      if (pos <= _lower && pos !== 0) {
        let _prevHint = found.clone()
        _prevHint.movePrev()
        if (!_prevHint.atTree() && this.equaler(_prevHint, _newProp)) {
          found = this.merge(this.tree, _prevHint)
        }
      }
    }
    if (_upper >= (pos + length)) {
      if (_upper == (pos + length)) {
        // 改变的区域结束正好在句结束位置，这时尝试向后合并句
        let _nextHint = found.clone()
        _nextHint.moveNext()
        if (!_nextHint.atTree() && this.equaler(_nextHint, _newProp)) {
          found = this.merge(this.tree, found)
        }
      }
      break
    }
    found.moveNext()
  }
}

参考链接

维基百科·红黑树
红黑树详细分析，看了都说好